Наука та освіта
Інтерактивні методи розв'язання задачі багатокритеріальної оптимізації. огляд
автор: Шварц Д. Т.
УДК 519.6
Росія, МГТУ ім. Н.е. Баумана
Більшість сучасних завдань проектування є багатокритеріальної. З розвитком виробництва і техніки число таких завдань постійно зростає. Наприклад, в компаніях НВО «Сатурн», ОКБ «Сухий», ТОВ «Ладуга», Canon, BMW, Fiat, Toyota, Piaggio процес проектування технічних об'єктів і систем нерозривно пов'язаний із застосуванням методів вирішення задачі багатокритеріальної оптимізації (МКО-завдання).
Методи рішення МКО-завдання надзвичайно різноманітні. Існує кілька способів класифікації цих методів [1, 2]. Наведемо класифікацію, засновану на зміст і форму використання додаткової інформації про переваги ОПР [2], відповідно до якої виділяють наступні класи методів:
· Методи, що не враховують переваги ОПР (no - preference methods);
· Апостеріорні методи (a posteriori methods);
· Апріорні методи (a priori methods);
· Інтерактивні методи (interactive methods).
Методи кожного з цих класів мають свої переваги і жоден з них не вільний від недоліків. Методи можуть належати різним класам, також можливі різні комбінації зазначених методів.
Методи, які не враховують переваги ОПР. Методи, що належать до даного класу, не передбачають врахування в тій чи іншій формі інформації про переваги ОПР. Тому завдання полягає в пошуку деякого компромісного рішення, зазвичай в «центральній частині» фронту Парето. Як приклади наведемо метод глобального критерію і метод нейтрального компромісного рішення [3].
Апостеріорні методи передбачають внесення ЛПР в МКО-систему інформації про свої уподобання після того, як отримано деякий безліч недомініруемих рішень. У зв'язку з цим все методи даного класу на першому етапі будують апроксимацію безлічі Парето. В роботі [4] виконано огляд сучасних методів Парето-апроксимації. Зазвичай для апроксимації фронту Парето використовують еволюційні алгоритми [5]. В роботі [6] виконано огляд основних напрямків розвитку еволюційних алгоритмів, покликаних підвищити їх ефективність в задачах оптимізації з великим числом критеріїв.
Основний недолік апостеріорного методів полягає в тому, що рівномірна апроксимація безлічі і / або фронту Парето вимагає великих обчислювальних витрат. Крім того, з підвищенням точності апроксимації, яку досягають збільшенням числа недомініруемих рішень, завдання вибору єдиного рішення з представленого безлічі стає більш трудомісткою для ЛПР. Нарешті, виникає самостійна проблема візуалізації фронту Парето для задач з числом критеріїв великим двох [7].
Апріорні методи покликані подолати основний недолік апостеріорного методів, пов'язаний з побудовою всієї множини досяжності. Тут припускають, що ЛПР вносить додаткову інформацію про свої уподобання до початку виконання завдання, апріорі. Найчастіше цю інформацію формалізують таким чином, щоб звести многокритериальную завдання до однокритерійним. Як приклади можна привести метод скалярної згортки, метод 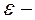 обмежень, лексикографічного впорядкування і цільового програмування [8, 9, 10].
обмежень, лексикографічного впорядкування і цільового програмування [8, 9, 10].
На практиці апріорні методи в «чистому» вигляді використовуються не часто, в зв'язку з тим, що часто ЛПР дуже складно сформулювати свої переваги перш ніж розпочати розв'язання завдання.
Інтерактивні методи. Методи даного классасостоят з сукупності ітерацій, кожна з яких включає в себе етап аналізу, що виконується ЛПР, і етап розрахунку, що виконується МКО-системою. За характером інформації, одержуваної МКО-системою від ЛПР на етапі аналізу, можна виділити класи інтерактивних методів [2], в яких ЛПР
· Безпосередньо призначає вагові коефіцієнти приватних критеріїв оптимальності;
· Накладає обмеження на значення приватних критеріїв оптимальності;
· Виконує оцінку пропонованих МКО-системою альтернатив.
У російськомовній літературі поряд з терміном інтерактивність методів багатокритеріальної оптимізації використовують термін адаптивність, роблячи акцент на тому, що методи повинні гарантувати отримання ефективного вирішення [2].
Основою для розвитку сучасних інтерактивних методів вирішення МКО-завдання послужили метод Дайера-Джіоффріона, метод SIGMOP (Sequential Information Generator for Multiple Objective Problems), метод Зайонца-Валленіуса [1, 2, 11].
Одним із сучасних інтерактивних методів багатокритеріальної оптимізації, який відноситься до класу методів із застосуванням інформації від ОПР про бажаних рівнях критеріїв, є метод NIMBUS (Nondifferentiable Interactive Multiobjective Bundle - based optimization System). Цей метод розроблений в Гельсінському університеті (м Гельсінкі, Фінляндія) під керівництвом професора К. Мієттінена і ін. [12].
Серед інтерактивних методів вирішення МКО-завдання найбільш перспективними є методи, засновані на оцінках рішень. Залежно від того, в якій формі ЛПР проводить оцінку рішень, до даного класу методів можна віднести
· Методи, в яких ЛПР виконує оцінку рішень в термінах «відмінно», «дуже добре», «добре» і т.д., або методи, засновані на оцінках функції переваг;
· Методи, в яких ЛПР виконує оцінку рішень в термінах «краще», «гірше», «однаково», або методи, засновані на парному порівнянні рішень.
Для ОПР ці форми завдання переваг є найбільш простими і зручними. В останні роки намітилися тенденції розвитку саме цього класу методів, що обумовлено необхідністю активної участі ОПР у вирішенні складних сучасних інженерних задач. Метою даної статті є огляд новітніх інтерактивних методів саме цього класу.
У першому розділі представлена постановка МКО-завдання. У другому і в третьому розділах розглядаються інтерактивні методи, засновані на оцінках функції переваг, і інтерактивні методи, засновані на парному порівнянні рішень, відповідно. У висновку сформульовані основні висновки.
МКО-завдання розглядаємо у вигляді
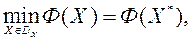
(1)
де 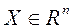 вектор змінних параметрів;
вектор змінних параметрів; 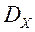 - обмежене і замкнутий безліч допустимих значень цього вектора;
- обмежене і замкнутий безліч допустимих значень цього вектора; 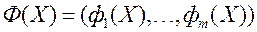 - векторний критерій оптимальності. ЛПР прагне знайти такий вектор
- векторний критерій оптимальності. ЛПР прагне знайти такий вектор 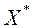 - шукане рішення МКО-завдання, який мінімізує на безлічі
- шукане рішення МКО-завдання, який мінімізує на безлічі 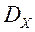 кожен з приватних критеріїв оптимальності.
кожен з приватних критеріїв оптимальності.
Безліч, в яке векторний критерій оптимальності 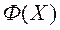 відображає безліч
відображає безліч 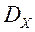 , позначимо
, позначимо 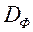 і назвемо критеріальним безліччю (безліччю досяжності).
і назвемо критеріальним безліччю (безліччю досяжності).
також позначимо 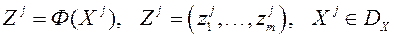 , І будемо писати
, І будемо писати 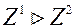 , якщо
, якщо 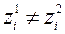 і серед рівностей і нерівностей
і серед рівностей і нерівностей 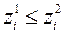 ,
, 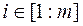 є, хоча б одне суворе. вектор
є, хоча б одне суворе. вектор 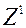 з критериального безлічі домінує по Парето вектор
з критериального безлічі домінує по Парето вектор 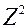 з того ж безлічі, якщо
з того ж безлічі, якщо 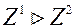 .
.
Чи не формально, безліч Парето 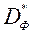 поставленої задачі багатокритеріальної оптимізації можна визначити як сукупність векторів
поставленої задачі багатокритеріальної оптимізації можна визначити як сукупність векторів 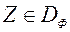 , Серед яких немає домінованих. Формально, безліч Парето визначають наступним чином:
, Серед яких немає домінованих. Формально, безліч Парето визначають наступним чином:
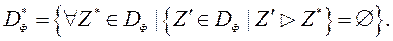
якщо 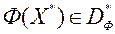 , То будемо говорити, що
, То будемо говорити, що 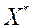 - ефективний по Парето вектор. Безліч векторів, що належать безлічі Парето, позначимо
- ефективний по Парето вектор. Безліч векторів, що належать безлічі Парето, позначимо 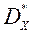 .
.
Інтерактивні методи вирішення МКО-завдання засновані на гіпотезі існування єдиної, невідомої ЛПР скалярної функції його переваг 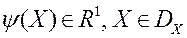 . При цьому вважають, що більшого значення функції
. При цьому вважають, що більшого значення функції 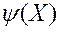 відповідає більш детально визначений з точки зору ОПР рішення
відповідає більш детально визначений з точки зору ОПР рішення 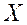 .
.
Метод FFANN. Перший інтерактивний метод багатокритеріальної оптимізації з використанням нейронних мереж для апроксимації функції переваг ОПР FFANN (Feed - Forward Artificial Neural Networks, метод з використанням штучної нейронної мережі прямого поширення) був розроблений професором Мінге Сан Університету Техасу (м Сан Антоніо, США) і професорами Антоніо Стам і Ральф Штойер Університету штату Джорджія (м Атланта, США) [13].
У методі FFANN ЛПР оцінює надані йому рішення, задаючи конкретні значення своєї функції переваг по кожному окремому рішенню. Для полегшення процедури оцінки, на кожній ітерації йому надають вектор надира 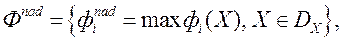 якому відповідає значення функції переваг
якому відповідає значення функції переваг 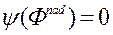 , І ідеальний вектор
, І ідеальний вектор 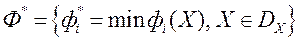 з оцінкою
з оцінкою 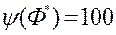 .
.
Структура нейронний мережі представлена на малюнку 1. Входами нейронний мережі є компоненти нормалізованого вектора приватних критеріїв оптимальності, виходом - значення функції переваг. Автори цього методу провели ряд експериментів, які підтверджують той факт, що метод є робастних до вибору архітектури нейронної мережі, точніше кажучи, - до числа нейронів в прихованому шарі.
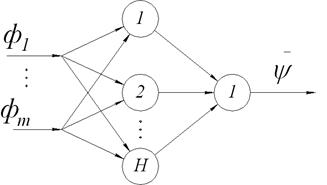
Малюнок 1 - Архітектура нейронної мережі в методі FFANN
Метод FFANN складається з наступних кроків.
Крок 1. Генеруємо s недомініруемих векторів 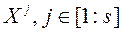 в безлічі допустимих значень
в безлічі допустимих значень 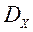 . Обчислюємо значення відповідного векторного критерію оптимальності
. Обчислюємо значення відповідного векторного критерію оптимальності 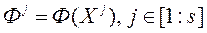 . Ініціалізіруем лічильник числа ітерацій
. Ініціалізіруем лічильник числа ітерацій 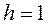 .
.
Крок 2. Надаємо s значень векторного критерію оптимальності 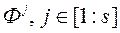 спільно з векторами
спільно з векторами 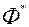 і
і 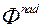 для оцінки ЛПР. На основі отриманої інформації про переваги ОПР, визначаємо найкращий вектор
для оцінки ЛПР. На основі отриманої інформації про переваги ОПР, визначаємо найкращий вектор 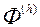 , Знайдений серед всіх ітерацій. Якщо ОПР задовольняє поточний найкраще рішення, то дане рішення ЛПР приймає в якості рішення МКО-завдання і припиняє обчислення.
, Знайдений серед всіх ітерацій. Якщо ОПР задовольняє поточний найкраще рішення, то дане рішення ЛПР приймає в якості рішення МКО-завдання і припиняє обчислення.
Крок 3. Нормалізуємо компоненти кожного з s критеріальних векторів за формулою
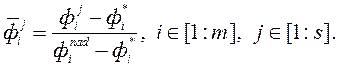
Крок 4. Після того як ЛПР призначив кожному рішенню значення своєї функції переваг 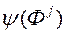 , Виконуємо нормалізацію його оцінок:
, Виконуємо нормалізацію його оцінок:
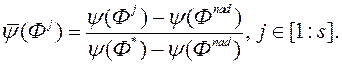
Крок 5. Використовуючи нормалізовані вектори 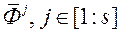 з відповідними нормалізованими оцінками
з відповідними нормалізованими оцінками 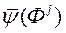 виконуємо навчання нейронної мережі FFANN.
виконуємо навчання нейронної мережі FFANN.
Крок 6. Використовуючи виходи нейронної мережі FFANN для обчислення значень цільової функції, вирішуємо завдання оптимізації для отримання нового вектора рішень на поточній h -ої ітерації:
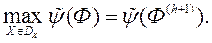
Крок 7. Якщо значення векторного критерію оптимальності 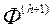 є унікальним, тобто його не надавали ОПР для оцінки на попередніх ітераціях, то генеруємо нові недомініруемих рішення, число яких дорівнює (s -1). В іншому випадку, ігноруємо
є унікальним, тобто його не надавали ОПР для оцінки на попередніх ітераціях, то генеруємо нові недомініруемих рішення, число яких дорівнює (s -1). В іншому випадку, ігноруємо 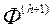 і генеруємо s нових рішень. Переходимо на Крок 2.
і генеруємо s нових рішень. Переходимо на Крок 2.
Для генерації недомініруемих рішень автори методу пропонують використовувати розширену зважену згортку Чебишева (augmented weighted Tchebycheff program)
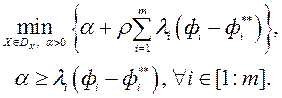
тут 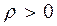 мала позитивна константа; утопічний вектор
мала позитивна константа; утопічний вектор 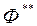 має координати
має координати 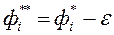 , де
, де 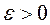 мала позитивна константа. Область допустимих значень вектора вагових множників
мала позитивна константа. Область допустимих значень вектора вагових множників 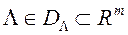 має вигляд
має вигляд 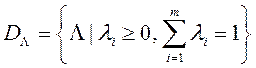 . Навчання нейронної мережі відбувається стандартним методом зворотного поширення помилки.
. Навчання нейронної мережі відбувається стандартним методом зворотного поширення помилки.
Основним недоліком даного методу є те, що рішення, які генеруються нейронною мережею, не завжди є Парето оптимальними. Для вирішення цієї проблеми автори методу FFANN запропонували модифікований варіант даного методу, який носить назву FFANN -2 [14].
Метод FFANN -2. Коротко розглянемо основні відмінності модифікованого методу FFANN -2 від його оригінальної версії. У методі FFANN -2 довільним чином генеруємо 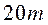 вагових векторів
вагових векторів 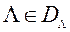 , Де m - число приватних критеріїв оптимальності. Автори методу рекомендують використовувати число рішень рівне
, Де m - число приватних критеріїв оптимальності. Автори методу рекомендують використовувати число рішень рівне 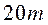 , На основі проведеного ними емпіричного дослідження. далі серед
, На основі проведеного ними емпіричного дослідження. далі серед 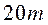 вагових векторів вибираємо 2 s вектора найбільш віддалених одна від одної на фронті Парето. Після цього, використовуючи вихід навченої нейронної мережі
вагових векторів вибираємо 2 s вектора найбільш віддалених одна від одної на фронті Парето. Після цього, використовуючи вихід навченої нейронної мережі 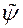 в якості значення функції переваг ОПР, обчислюємо значення функції
в якості значення функції переваг ОПР, обчислюємо значення функції 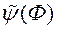 при подачі на вхід 2 s векторів
при подачі на вхід 2 s векторів 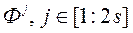 . Серед всіх отриманих значень
. Серед всіх отриманих значень 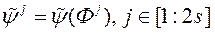 вибираємо s векторів
вибираємо s векторів 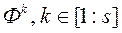 , Які забезпечують максимальне значення
, Які забезпечують максимальне значення 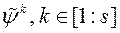 .
.
У даній версії методу нейронна мережа, яка реалізує апроксимацію функції переваг ОПР, не бере участі в пошуку найкращого з точки зору ОПР рішення, вона всього лише є оператор, який підтримує різноманітність рішень, що надаються ЛПР для оцінки.
Метод PREF (PREFerence) покликаний вирішити вищевказані недоліки методів FFANN. Даний метод був розроблений автором огляду під керівництвом д.ф.-м.н. Карпенко А.П. в МГТУ ім. Н.е. Баумана [15].
В основі методу PREF лежить операція скалярної згортки приватних критеріїв оптимальності 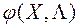 , де
, де 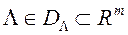 - вектор вагових множників,
- вектор вагових множників, 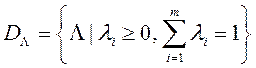 - безліч допустимих значень цього вектора. Спосіб згортки не фіксується - це може бути аддитивная згортка, мультиплікативна згортка і інші.
- безліч допустимих значень цього вектора. Спосіб згортки не фіксується - це може бути аддитивная згортка, мультиплікативна згортка і інші.
При кожному фіксованому векторі 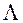 метод скалярної згортки зводить рішення багатокритеріальної задачі (1) до вирішення однокритерійним завдання глобальної умовної оптимізації (ОКО-завдання)
метод скалярної згортки зводить рішення багатокритеріальної задачі (1) до вирішення однокритерійним завдання глобальної умовної оптимізації (ОКО-завдання)
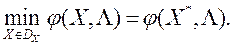
(2)
В силу обмеженості і замкнутості безлічі 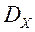 рішення задачі (2) існує.
рішення задачі (2) існує.
Якщо при кожному 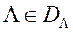 рішення задачі (2) єдино, то умова (2) ставить у відповідність кожному з допустимих векторів
рішення задачі (2) єдино, то умова (2) ставить у відповідність кожному з допустимих векторів 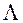 єдиний вектор
єдиний вектор 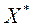 і відповідні значення приватних критеріїв оптимальності
і відповідні значення приватних критеріїв оптимальності 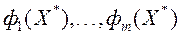 . Ця обставина дозволяє вважати, що функція переваг ОПР
. Ця обставина дозволяє вважати, що функція переваг ОПР 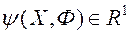 визначена не на безлічі
визначена не на безлічі 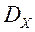 , А на безлічі
, А на безлічі 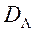 .
.
Основна ідея методу PREF полягає в побудові апроксимації функції переваг ОПР 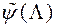 на безлічі
на безлічі 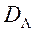 і пошуку вектора
і пошуку вектора 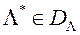 , Який максимізує функцію переваг ОПР. Більш строго, вектор
, Який максимізує функцію переваг ОПР. Більш строго, вектор 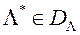 знаходимо в результаті рішення ОКО-завдання
знаходимо в результаті рішення ОКО-завдання
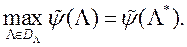
Перехід з простору змінних параметрів 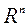 , В простір вагових множників
, В простір вагових множників 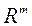 , Дозволяє спростити пошук найкращого з точки зору ОПР рішення, оскільки, як правило
, Дозволяє спростити пошук найкращого з точки зору ОПР рішення, оскільки, як правило 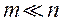 .
.
Ключовий процедурою в методі PREF є апроксимація функції переваг. Для апроксимації функції переваг в роботі [15] запропоновано використовувати нейронні мережі, апарат нечіткої логіки та нейро-нечіткі системи.
Загальна схема методу PREF є ітераційної і складається з наступних основних етапів.
Етап «розгону» методу. МКО-система певним чином (наприклад, випадково) послідовно генерує k векторів 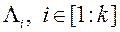 і для кожного з цих векторів виконує наступні дії.
і для кожного з цих векторів виконує наступні дії.
1) Вирішує ОКО-завдання
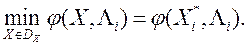
(3)
2) Чи пред'являє ЛПР знайдене рішення 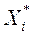 , А також відповідні значення всіх приватних критеріїв оптимальності
, А також відповідні значення всіх приватних критеріїв оптимальності 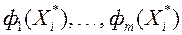 .
.
3) ЛПР оцінює ці дані і вводить в МКО-систему відповідне значення своєї функції переваг 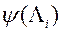 .
.
Перший етап. На основі всіх наявних в МКО-системі значень 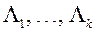 вектора
вектора 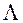 і відповідних оцінок функції переваг
і відповідних оцінок функції переваг 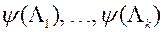 МКО-система виконує наступні дії.
МКО-система виконує наступні дії.
1) Будує функцію 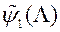 , Аппроксимирующую функцію
, Аппроксимирующую функцію 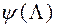 в околиці точок
в околиці точок 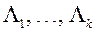 .
.
2) Шукає максимум функції 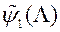 - вирішує ОКО-завдання
- вирішує ОКО-завдання
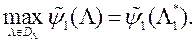
3) Зі знайденим вектором 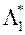 вирішує ОКО-завдання виду (3) - знаходить вектор параметрів і відповідні значення приватних критеріїв оптимальності, а потім пред'являє їх ЛПР. У свою чергу, ЛПР оцінює запропоновані йому рішення і вводить в систему відповідне значення своєї функції переваг
вирішує ОКО-завдання виду (3) - знаходить вектор параметрів і відповідні значення приватних критеріїв оптимальності, а потім пред'являє їх ЛПР. У свою чергу, ЛПР оцінює запропоновані йому рішення і вводить в систему відповідне значення своєї функції переваг 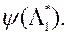
Другий етап. На основі всіх наявних в системі значень вектора 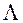 і відповідних оцінок функції переваг
і відповідних оцінок функції переваг 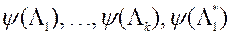 МКО-система виконує апроксимацію функції
МКО-система виконує апроксимацію функції 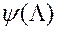 в околиці точок
в околиці точок 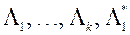 - будує функцію
- будує функцію 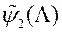 . І так далі за схемою першого етапу до тих пір, поки ЛПР не зупиниться на якомусь рішенні.
. І так далі за схемою першого етапу до тих пір, поки ЛПР не зупиниться на якомусь рішенні.
Таким чином, в методі PREF на етапі аналізу ЛПР для оцінки надаються рішення, що належать безлічі Парето. На етапі розрахунку для пошуку більш задовільних з точки зору ОПР рішень безпосередньо використовується апроксимація функції переваг ОПР.
Особливості нейросетевой, нечіткою і нейро-нечіткої апроксимації функції переваг ОПР розглядаються в роботах [16, 17, 18]. Також в цих роботах проведено дослідження ефективності зазначених способів апроксимації при вирішенні тестових МКО-завдань. Результати вирішення практичних завдань з використанням методу PREF представлені в роботах [16, 19].
В даному класі методів припускають, що ЛПР вносить свої переваги в МКО-систему у вигляді парного порівняння окремих рішень [20, 21, 22]. Наприклад, альтернатива ![В даному класі методів припускають, що ЛПР вносить свої переваги в МКО-систему у вигляді парного порівняння окремих рішень [20, 21, 22]](/wp-content/uploads/2019/12/uk-nauka-ta-osvita-90.gif) і відповідне значення векторного критерію оптимальності
і відповідне значення векторного критерію оптимальності 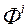 «Краще» набору
«Краще» набору 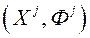 (Позначимо,
(Позначимо, 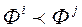 ) Або два набори
) Або два набори 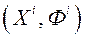 і
і 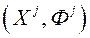 «Невиразні»
«Невиразні» 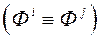 . На основі отриманої інформації МКО-система той чи інший спосіб будує апроксимацію функції переваг ОПР
. На основі отриманої інформації МКО-система той чи інший спосіб будує апроксимацію функції переваг ОПР 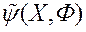 з метою забезпечення коректного ранжирування даних. Іншими словами, якщо
з метою забезпечення коректного ранжирування даних. Іншими словами, якщо 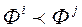 , то
, то 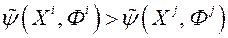 ; якщо
; якщо 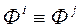 , то
, то 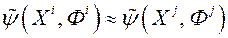 .
.
Всі методи даного класу, розроблені до теперішнього часу, використовують близький підхід, який полягає в комбінації одного з еволюційних алгоритмів з процедурою побудови функції переваг ОПР 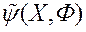 .
.
Загальна схема методів даного класу може бути представлена наступним чином.
Крок 1. Генеруємо початкову популяцію рішень 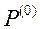 .
.
Крок 2. Одним з методів наближеного побудови безлічі Парето отримуємо початкову апроксимацію цієї множини: формуємо безліч рішень 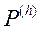 .
.
Крок 3. Вибираємо з безлічі 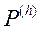 число рішень
число рішень 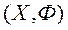 рівне s для оцінки ЛПР. Потім ЛПР ранжує ці рішення і вносить цю інформацію в систему.
рівне s для оцінки ЛПР. Потім ЛПР ранжує ці рішення і вносить цю інформацію в систему.
Крок 4. На основі отриманої інформації МКО-система будує апроксимацію функції переваг ОПР 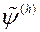 .
.
Крок 5. Запускаємо метод наближеного побудови безлічі Парето, при цьому, як «функції пристосованості» окремих рішень використовуємо поточну функцію переваг ОПР 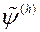 і формуємо безліч рішень
і формуємо безліч рішень 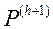 .
.
Крок 6. Якщо умова зупинки виконана, то завершуємо обчислення. В іншому випадку, здійснюємо перехід на Крок 2.
Основним критерієм зупинки є отримання ЛПР найбільш задовольняє його рішення. Однак на етапі випробування методу на тестових завданнях багатокритеріальної оптимізації, при відсутності реального ЛПР, можуть бути розглянуті також інші умови. Наприклад, виконання наперед заданого числа ітерацій діалогу з ОПР або досягнення фіксованого числа ітерацій методу наближеного побудови безлічі Парето.
Далі в роботі розглядаємо найбільш розвинені сучасні методи даного класу: IEM, PI - EMO - VF, BC - EMO.
Метод IEM. В роботі [20] автори пропонують метод IEM (Interactive Evolutionary Method, Інтерактивний еволюційний метод), в основі якого лежить скалярная згортка приватних критеріїв оптимальності виду
![В роботі [20] автори пропонують метод IEM (Interactive Evolutionary Method, Інтерактивний еволюційний метод), в основі якого лежить скалярная згортка приватних критеріїв оптимальності виду](/wp-content/uploads/2019/12/uk-nauka-ta-osvita-105.gif)
(4)
де 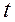 - параметр, який визначає функцію переваг;
- параметр, який визначає функцію переваг; 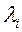 - компоненти вектора вагових множників
- компоненти вектора вагових множників 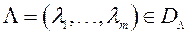 ;
; 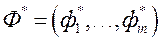 - ідеальний вектор приватних критеріїв оптимальності. Для знаходження вагових множників
- ідеальний вектор приватних критеріїв оптимальності. Для знаходження вагових множників 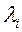 автори вирішують задачу оптимізації
автори вирішують задачу оптимізації
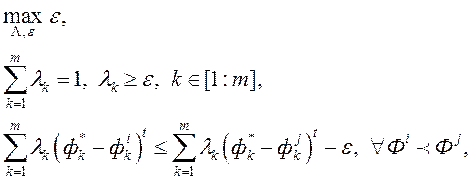
(5)
де 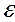 - «межа» переваг. Тут парні порівняння рішень формують обмеження задачі оптимізації. В роботі [20] автори припускають, що функція переваг ОПР лінійна (
- «межа» переваг. Тут парні порівняння рішень формують обмеження задачі оптимізації. В роботі [20] автори припускають, що функція переваг ОПР лінійна ( 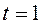 ). При цьому, автори не наводять жодних рекомендацій щодо вибору цього параметра. Якщо функція переваг нелінійна, то цей метод може генерувати неприпустимі для ЛПР рішення. В цьому випадку автори пропонують видаляти по одному з обмежень в хронологічному порядку, до тих пір, поки рішення задачі (5) не знайдено. Тим самим вони припускають, що останні надійшли оцінки від ЛПР мають б о більшу важливість, ніж інформація, отримана на перших ітераціях.
). При цьому, автори не наводять жодних рекомендацій щодо вибору цього параметра. Якщо функція переваг нелінійна, то цей метод може генерувати неприпустимі для ЛПР рішення. В цьому випадку автори пропонують видаляти по одному з обмежень в хронологічному порядку, до тих пір, поки рішення задачі (5) не знайдено. Тим самим вони припускають, що останні надійшли оцінки від ЛПР мають б о більшу важливість, ніж інформація, отримана на перших ітераціях.
Метод PI - EMO - VF (Progressively Interactive Evolutionary Multi - objective Optimization using Value Function, Інтерактивний Еволюційний метод Багатокритеріальний Оптимізації з використанням Функції Переваг) [21]. Тут автори пропонують використовувати функцію переваг виду
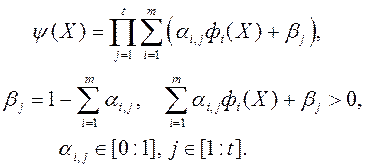
(6)
Параметр t також визначає функцію переваг ОПР. визначення коефіцієнтів 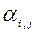 и
и 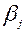 відбувається в результаті рішення допоміжної задачі
відбувається в результаті рішення допоміжної задачі
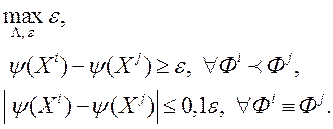
(7)
На відміну від методу IEM, тут враховується інформація про рішення, які для ЛПР рівнозначні. Іншою важливою відмінністю є те, що параметр 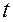 підбирають ітераційно. На першому етапі беруть
підбирають ітераційно. На першому етапі беруть 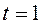 і вирішують задачу (7). Якщо в процесі вирішення цього завдання не вдається знайти коефіцієнти функції переваг (6) так, щоб задовольнити всіх обмежень, то параметр
і вирішують задачу (7). Якщо в процесі вирішення цього завдання не вдається знайти коефіцієнти функції переваг (6) так, щоб задовольнити всіх обмежень, то параметр 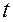 збільшують
збільшують 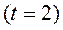 , І знову вирішують задачу (7). Обчислення виконують до тих пір, поки функція переваг не буде задовольняти всім обмеженням (7).
, І знову вирішують задачу (7). Обчислення виконують до тих пір, поки функція переваг не буде задовольняти всім обмеженням (7).
Метод PI - EMO - VF як метод апроксимації безлічі Парето використовує алгоритм NSGA - II (Non-dominated sorting genetic algorithm version II - Генетичний алгоритм недомініруемих сортування версії II) [23].
Автори методів IEM і PI - EMO - VF при побудові функції переваг не беруть до уваги те, що ЛПР може помилятися і давати суперечливі відповіді. Вони мають на увазі, що ЛПР завжди дає вірні оцінки і, в результаті, зводять задачу навчання до задачі оптимізації.
Метод BC - EMO (Brain - Computer Evolutionary Multiobjective Optimization, нейрокомп'ютерних Еволюційний метод багатокритеріальної оптимізації), з нашої точки зору, є найбільш перспективним в даний час [22]. Відзначимо, що переклад терміна «brain-computer» відповідає прийнятій термінології (http://neurobotics.ru/research/bci/). Апроксимацію функції переваг ![Метод BC - EMO (Brain - Computer Evolutionary Multiobjective Optimization, нейрокомп'ютерних Еволюційний метод багатокритеріальної оптимізації), з нашої точки зору, є найбільш перспективним в даний час [22]](/wp-content/uploads/2019/12/uk-nauka-ta-osvita-119.gif) в цьому методі виконують на основі машини опорних векторів (Support Vector Machine, SVM) [24], що вигідно відрізняє BC - EMO від інших існуючих інтерактивних методів даного класу:
в цьому методі виконують на основі машини опорних векторів (Support Vector Machine, SVM) [24], що вигідно відрізняє BC - EMO від інших існуючих інтерактивних методів даного класу:
1) метод дозволяє будувати функцію переваг на основі парних порівнянь рішень, ця форма оцінки рішень є найбільш зручною для ЛПР;
2) метод є робастних до неточних і суперечливим оцінками ЛПР, що є типовим при вирішенні МКО-завдань;
3) вибір різних ядер [24] в методі опорних векторів дозволяє найкращим способом апроксимувати функцію переваг ОПР.
У методі BC - EMO функція переваг ОПР будується в вигляді 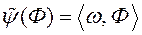 , Де символ
, Де символ 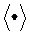 позначає скалярний добуток векторів. Ця функція повинна виконувати заданий ранжування даних:
позначає скалярний добуток векторів. Ця функція повинна виконувати заданий ранжування даних: 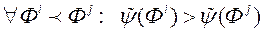 . Для побудови функції переваг ОПР необхідно знайти такий вектор
. Для побудови функції переваг ОПР необхідно знайти такий вектор 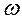 , Який задовольняє всім нерівностям виду
, Який задовольняє всім нерівностям виду
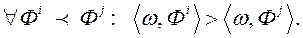
(8)
При вирішенні практичних завдань дуже складно підібрати такий вектор 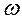 , Який задовольняє всім вищевказаним неравенствам (8). В цьому випадку, точки з простору критеріїв проектують в новий простір ознак (feature space) за допомогою проецирующей функції
, Який задовольняє всім вищевказаним неравенствам (8). В цьому випадку, точки з простору критеріїв проектують в новий простір ознак (feature space) за допомогою проецирующей функції 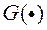 . Новий простір має велику розмірність, ніж розмірність простору критеріїв (це простір, в якому до вихідних ознаками - приватним критеріям оптимальності - додані їх парні твори). В математичному формулюванні завдання оптимізації для пошуку вектора
. Новий простір має велику розмірність, ніж розмірність простору критеріїв (це простір, в якому до вихідних ознаками - приватним критеріям оптимальності - додані їх парні твори). В математичному формулюванні завдання оптимізації для пошуку вектора 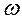 має вигляд
має вигляд
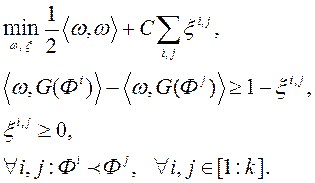
(9)
фіктивна змінна ![фіктивна змінна характеризує величину помилки на двох векторах и , З - параметр регуляризації, задається користувачем або адаптивно підбирається на основі перехресної перевірки (cross-validation) [22]](/wp-content/uploads/2019/12/uk-nauka-ta-osvita-127.gif) характеризує величину помилки на двох векторах
характеризує величину помилки на двох векторах 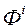 и
и 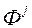 , З - параметр регуляризації, задається користувачем або адаптивно підбирається на основі перехресної перевірки (cross-validation) [22].
, З - параметр регуляризації, задається користувачем або адаптивно підбирається на основі перехресної перевірки (cross-validation) [22].
Завдання (9) є завданням квадратичного програмування, тому для її вирішення доцільно застосувати метод множників Лагранжа. Метод вимагає обчислення скалярного твори 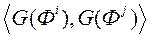 . Для ефективного обчислення скалярного добутку двох векторів без безпосереднього проектування їх в новий простір вводять поняття ядра скалярного твори і позначають його
. Для ефективного обчислення скалярного добутку двох векторів без безпосереднього проектування їх в новий простір вводять поняття ядра скалярного твори і позначають його 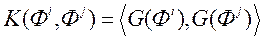 .
.
В результаті функцію переваг можна записати у вигляді лінійної комбінації ядер
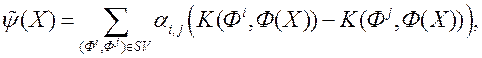
де ![де - множники Лагранжа [22]](/wp-content/uploads/2019/12/uk-nauka-ta-osvita-133.gif) - множники Лагранжа [22].
- множники Лагранжа [22].
У методі BC - EMO вибір конкретної функції ядра відбувається автоматично в процесі рішення МКО-завдання на основі перехресної перевірки з наступного списку:
· 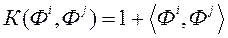 - лінійна функція;
- лінійна функція;
· 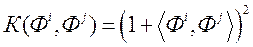 - поліноміальна функція другого ступеня;
- поліноміальна функція другого ступеня;
· 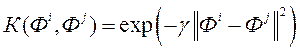 - Функція Гауса, де позитивну константу
- Функція Гауса, де позитивну константу 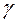 підбирають із сукупності
підбирають із сукупності 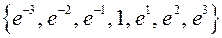 .
.
Оригінальна версія BC - EMO, також як метод PI - EMO - VF, як метод апроксимації безлічі Парето використовує алгоритм NSGA - II [23].
Результати широкого дослідження ефективності методу BC - EMO на різних тестових МКО-завданнях наведені в роботі [22].
В роботі виконано огляд сучасних інтерактивних методів FFANN і PREF, заснованих на оцінках функції переваг, і методів IEM, PI - EMO - VF і BC - EMO, заснованих на парному порівнянні рішень.
На підставі виконаного огляду може бути зроблений висновок про те, що найбільш перспективними є методи PREF і BC - EMO. Пропонуються наступні напрямки розвитку цих методів.
· Розробка більш зручних засобів взаємодії ЛПР з зазначеними методами; створення самостійної МКО-системи на основі цих методів.
· Розробка і реалізація паралельних алгоритмів методів PREF і BC - EMO в зв'язку з тим, що практичні завдання оптимізації, як правило, мають велику обчислювальну складність.
Автор дякує свого наукового керівника д.ф.-м.н. МГТУ ім.Н.Е. Баумана Карпенко А.П. за плідне обговорення роботи, а також за всебічну допомогу щодо її вдосконалення.
Список літератури
1. Лотов А.В., Поспєлова І.І. Багатокритеріальні задачі прийняття рішень: навч. посібник. М .: МАКС Пресс, 2008. 197 c.
2. Растригин Л.А., Ейдук Я.Ю. Адаптивні методи багатокритеріальної оптимізації // Автоматика і телемеханіка. 1985. № 1. З. 5-26.
3. Wierzbicki AP Reference point approaches // Multicriteria Decision Making: Advances in MCDM Models, Algorithms, Theory and Applications / Gal T., Stewart TJ, Hanne T. (Eds.). Boston: Kluwer Academic Publishers, 1999. P. 9.1-9.39.
4. Карпенко А. П., Семеніхін А. С., Мітіна Е. В. Популяційні методи апроксимації безлічі Парето в завданню багатокритеріальної оптимізації. Огляд // Наука і освіта. МГТУ ім. Н.е. Баумана. Електрон. журн. 2012. № 4. Режим доступу: http://www.technomag.edu.ru/doc/363023.html (Дата звернення 08.07.2012).
5. Multiobjective Optimization: Interactive and Evolutionary Approaches / Branke J., Deb K., Miettinen K., Slowinski R. (Eds.). Berlin / Heidelberg, Germany: Springer-Verlag, 2008. 470 p.
6. Wang R., Purshouse RC, Fleming PJ Preference-inspired Co-evolutionary Algorithms for Many-objective Optimisation // IEEE Transactions on Evolutionary Computation. 2012. DOI: 10.1109 / TEVC.2012.2204264
7. Miettinen K. Nonlinear Multiobjective Optimization. Boston: Kluwer Academic Publishers, 1999. 298 p.
8. Gass S., Saaty T. The computational algorithm for the parametric objective function // Naval Research Logistics Quarterly. Wiley, 1955. Vol. 2, no. 1-2. P. 39-45.
9. Fishburn PC Lexicographic orders, utilities and decision rules: A survey // Management Science. USA, 1974. Vol. 20, no. 11. P. 1442-1471.
10. Charnes A., Cooper WW Management Models and Industrial Applications of Linear Programming. Vol. 1. New York: Wiley, 1961. 859 p.
11. Ларичев О.І. Теорія і методи прийняття рішень. М .: Університетська книга, Логос, 2002. 392 c.
12. Miettinen K., Makela MM Interactive Bundle-based Method for Nondifferentiable Multiobjective Optimization: NIMBUS // Optimization: A Journal of Mathematical Programming and Operations Research. 1995. Vol. 34, no. 3. P. 231-246.
13. Sun M., Stam A., Steuer R. Solving multiple objective programming problems using feed-forward artificial neural networks: The interactive FFANN procedure // Management Science. 1996. Vol. 42, no. 6. P. 835-849.
14. Sun M., Stam A., Steuer R. Interactive multiple objective programming using Tchebycheff programs and artificial neural networks // Computer Operations Research. 2000. Vol. 27, no. 7-8. P. 601-620.
15. Карпенко А.П., Федорук В.Г. Апроксимація функції переваг особи, що приймає рішення, в завданню багатокритеріальної оптимізації. 3. Методи на основі нейронних мереж і нечіткої логіки // Наука і освіта. МГТУ ім. Н.е. Баумана. Електрон. журн. 2008. № 4. Режим доступу: http://www.technomag.edu.ru/doc/86335.html (Дата звернення 02.07.2012).
16. Карпенко А.П., Мухлісулліна Д.Т., Овчинников В.А. Нейросетевая апроксимація функції переваг особи, що приймає рішення, в завданню багатокритеріальної оптимізації // Інформаційні технології. 2010. № 10. С. 2-9.
17. Карпенко А.П., Моор Д.А., Мухлісулліна Д.Т. Багатокритерійна оптимізація на основі нечіткої апроксимації функції переваг особи, що приймає рішення // Високі технології та інтелектуальні системи 2010: Додати праці 12-ої молодіжної міжнародної науково-технічної конференції. М., 2010. С. 94-98.
18. Карпенко А.П., Моор Д.А., Мухлісулліна Д.Т. Багатокритерійна оптимізація на основі нейро-нечіткої апроксимації функції переваг особи, що приймає рішення // Наука і освіта. МГТУ ім. Н.е. Баумана. Електрон. журн. 2010. № 6. Режим доступу: http://technomag.edu.ru/doc/143964.html (Дата звернення 03.10.2012).
19. Карпенко А.П., Мухлісулліна Д.Т., Цвєтков А.А. Багатокритерійна оптимізація геометрії щілинного фільтра для очищення рідин // Наука і освіта. МГТУ ім. Н. Е. Баумана. Електрон. журн. 2013. № 2. DOI: 10.7463 / 0213.0539055
20. Phelps S., Koksalan M. An interactive evolutionary metaheuristic for multiobjective combinatorial optimization // Management Science. 2003. Vol. 49, no. 12. P. 1726-1738.
21. Deb K., Sinha A., Korhonen PJ, Wallenius J. An Interactive Evolutionary Multiobjective Optimization Method Based on Progressively Approximated Value Function // IEEE Transactions on Evolutionary Computation. 2010. Vol. 14, no. 5. P. 723-739.
22. Battiti R., Passerini A. Brain-computer evolutionary multiobjective optimization (BC-EMO): a genetic algorithm adapting to the decision maker // IEEE Transaction on Evolutionary Computation. 2010. Vol. 14, no. 5. P. 671-687.
23. Deb K., Pratap A., Agarwal S., Meyarivan T. A fast elitist multi-objective genetic algorithm: NSGA-II // IEEE Transaction on Evolutionary Computation. 2002. Vol. 6, no. 2. P. 182-197.
24. Хайкін С. Нейронні мережі. Повний курс: пров. з англ. М .: ТОВ «І.Д.Вільямс», 2008. 1104 c.
25. Zhang Q., Li H. MOEA / D: A multiobjective evolutionary algorithm based on decomposition // IEEE Transactions on Evolutionary Computation. 2007. Vol. 11, no. 6. P. 712-731.
26. Li H., Zhang Q. Multiobjective optimization problems with complicated pareto sets, MOEA / D and NSGA-II // IEEE Transactions on Evolutionary Computation. 2009. Vol. 13, no. 2. P. 284-302.
