НАВУКА і АДУКАЦЫЮ
Інтэрактыўныя метады рашэння задачы многокритериальной аптымізацыі. Агляд
аўтар: Шварц Д. Т.
УДК 519.6
Расія, МГТУ ім. Н.Э. Баумана
Большасць сучасных задач праектавання з'яўляюцца многокритериальными. З развіццём вытворчасці і тэхнікі лік такіх задач пастаянна расце. Напрыклад, у кампаніях НВА "Сатурн", ОКБ "Сухі", ТАА «Ладуга», Canon, BMW, Fiat, Toyota, Piaggio працэс праектавання тэхнічных аб'ектаў і сістэм непарыўна звязаны з ужываннем метадаў рашэння задачы многокритериальной аптымізацыі (МКО-задачы).
Метады рашэння МКО-задачы надзвычай разнастайныя. Існуе некалькі спосабаў класіфікацыі гэтых метадаў [1, 2]. Прывядзём класіфікацыю, заснаваную на змесце і форме выкарыстання дадатковай інфармацыі аб перавагах ЛПР [2], у адпаведнасці з якой вылучаюць наступныя класы метадаў:
· Метады, ня ўлічваюць перавагі ЛПР (no - preference methods);
· Апастэрыёрнае метады (a posteriori methods);
· Апрыёрныя метады (a priori methods);
· Інтэрактыўныя метады (interactive methods).
Метады кожнага з гэтых класаў маюць свае вартасці і ні адзін з іх не свабодны ад недахопаў. Метады могуць належаць розных класаў, таксама магчымыя розныя камбінацыі названых метадаў.
Метады, ня ўлічваюць перавагі ЛПР. Метады, якія належаць да дадзенага класа, не мяркуюць ўліку ў той ці іншай форме інфармацыі аб перавагах ЛПР. Таму задача складаецца ў пошуку некаторага кампраміснага рашэння, звычайна ў «цэнтральнай частцы» фронту Парэта. У якасці прыкладаў прывядзем метад глабальнага крытэра і метад нейтральнага кампраміснага рашэння [3].
Апастэрыёрнае метады мяркуюць ўнясенне ЛПР ў МКО-сістэму інфармацыі аб сваіх перавагах пасля таго, як атрымана некаторы мноства недоминируемых рашэнняў. У гэтай сувязі усе метады дадзенага класа на першым этапе будуюць апраксімацыю мноства Парэта. У працы [4] выкананы агляд сучасных метадаў Парэта-апраксімацыі. Звычайна для апраксімацыі фронту Парэта выкарыстоўваюць эвалюцыйныя алгарытмы [5]. У працы [6] выкананы агляд асноўных напрамкаў развіцця эвалюцыйных алгарытмаў, закліканых павысіць іх эфектыўнасць у задачах аптымізацыі з вялікім лікам крытэраў.
Асноўны недахоп апастэрыёрнае метадаў складаецца ў тым, што раўнамерная апраксімацыя мноства і / або фронту Парэта патрабуе вялікіх вылічальных выдаткаў. Акрамя таго, з павышэннем дакладнасці апраксімацыі, якую дасягаюць павелічэннем колькасці недоминируемых рашэнняў, задача выбару адзінага рашэння з прадстаўленага мноства становіцца больш працаёмкай для ЛПР. Нарэшце, узнікае самастойная праблема візуалізацыі фронту Парэта для задач з лікам крытэрыяў вялікім двух [7].
Апрыёрныя метады закліканы пераадолець асноўны недахоп апастэрыёрнае метадаў, звязаны з пабудовай усяго мноства дасяжнасці. Тут мяркуюць, што ЛПР ўносіць дадатковую інфармацыю аб сваіх перавагах да пачатку рашэння задачы, апрыёры. Часцей за ўсё гэтую інфармацыю фармалізуе такім чынам, каб звесці многокритериальную задачу да однокритериальной. У якасці прыкладаў можна прывесці метад скалярнай скруткі, метад 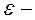 абмежаванняў, лексікаграфічныя упарадкавання і мэтавага праграмавання [8, 9, 10].
абмежаванняў, лексікаграфічныя упарадкавання і мэтавага праграмавання [8, 9, 10].
На практыцы апрыёрныя метады ў «чыстым» выглядзе выкарыстоўваюцца не часта, у сувязі з тым, што часцяком ЛПР вельмі складана сфармуляваць свае перавагі да пачатку рашэння задача.
Інтэрактыўныя метады. Метады дадзенага классасостоят з сукупнасці ітэрацый, кожная з якіх уключае ў сябе этап аналізу, які выконваецца ЛПР, і этап разліку, які выконваецца МКО-сістэмай. Па характары інфармацыі, якую атрымліваюць МКО-сістэмай ад ЛПР на этапе аналізу, можна вылучыць класы інтэрактыўных метадаў [2], у якіх ЛПР
· Непасрэдна прызначае вагавыя каэфіцыенты прыватных крытэрыяў аптымальнасці;
· Накладвае абмежаванні на значэння прыватных крытэрыяў аптымальнасці;
· Выконвае ацэнку прапанаваных МКО-сістэмай альтэрнатыў.
У рускамоўнай літаратуры нараўне з тэрмінам інтэрактыўнасць метадаў многокритериальной аптымізацыі выкарыстоўваюць тэрмін адаптыўнасць, робячы акцэнт на тым, што метады павінны гарантаваць атрыманне эфектыўнага рашэння [2].
Асновай для развіцця сучасных інтэрактыўных метадаў рашэння МКО-задачы паслужылі метад Дайер-Джиоффриона, метад SIGMOP (Sequential Information Generator for Multiple Objective Problems), метад Зайонц-Валлениуса [1, 2, 11].
Адным з сучасных інтэрактыўных метадаў многокритериальной аптымізацыі, які адносіцца да класа метадаў з ужываннем інфармацыі ад ЛПР аб жаданых узроўнях крытэрыяў, з'яўляецца метад NIMBUS (Nondifferentiable Interactive Multiobjective Bundle - based optimization System). Гэты метад распрацаваны ў Хельсінскім універсітэце (г. Хельсінкі, Фінляндыя) пад кіраўніцтвам прафесара К. Миеттинен і інш. [12].
Сярод інтэрактыўных метадаў рашэння МКО-задачы найбольш перспектыўнымі з'яўляюцца метады, заснаваныя на ацэнках рашэнняў. У залежнасці ад таго, у якой форме ЛПР вырабляе ацэнку рашэнняў, да дадзенага класа метадаў можна аднесці
· Метады, у якіх ЛПР выконвае ацэнку рашэнняў у тэрмінах «выдатна», «вельмі добра», «добра» і г.д., або метады, заснаваныя на ацэнках функцыі пераваг;
· Метады, у якіх ЛПР выконвае ацэнку рашэнняў у тэрмінах «лепш», «горш», «аднолькава», ці метады, заснаваныя на парным параўнанні рашэнняў.
Для ЛПР гэтыя формы заданні пераваг з'яўляюцца найбольш простымі і зручнымі. У апошнія гады намеціліся тэндэнцыі развіцця менавіта гэтага класа метадаў, што абумоўлена неабходнасцю актыўнага ўдзелу ЛПР ў вырашэнні складаных сучасных інжынерных задач. Мэтай дадзенага артыкула з'яўляецца агляд найноўшых інтэрактыўных метадаў менавіта гэтага класа.
У першым раздзеле прадстаўлена пастаноўка МКО-задачы. У другім і ў трэцім раздзелах разглядаюцца інтэрактыўныя метады, заснаваныя на ацэнках функцыі пераваг, і інтэрактыўныя метады, заснаваныя на парным параўнанні рашэнняў, адпаведна. У зняволенні сфармуляваны асноўныя высновы.
МКО-задачу разглядаем у выглядзе
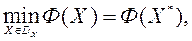
(1)
дзе 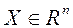 -вектор варьируемых параметраў;
-вектор варьируемых параметраў; 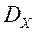 - абмежаванае і замкнёнае мноства дапушчальных значэнняў гэтага вэктару;
- абмежаванае і замкнёнае мноства дапушчальных значэнняў гэтага вэктару; 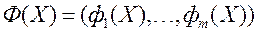 - вектарны крытэрый аптымальнасці. ЛПР імкнецца знайсці такі вектар
- вектарны крытэрый аптымальнасці. ЛПР імкнецца знайсці такі вектар 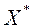 - шуканае рашэнне МКО-задачы, які мінімізуе на мностве
- шуканае рашэнне МКО-задачы, які мінімізуе на мностве 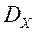 кожны з прыватных крытэрыяў аптымальнасці.
кожны з прыватных крытэрыяў аптымальнасці.
Мноства, у якое вектарны крытэрый аптымальнасці 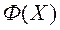 адлюстроўвае мноства
адлюстроўвае мноства 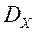 , пазначым
, пазначым 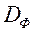 і назавем крытэрыяльна мноствам (мноствам дасяжнасці).
і назавем крытэрыяльна мноствам (мноствам дасяжнасці).
таксама пазначым 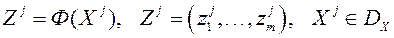 , І будзем пісаць
, І будзем пісаць 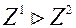 , калі
, калі 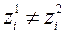 і сярод роўнасцяў і няроўнасцей
і сярод роўнасцяў і няроўнасцей 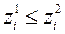 ,
, 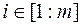 маецца, хоць бы адно строгае. вектар
маецца, хоць бы адно строгае. вектар 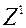 з крытэрыяльна мноства дамінуе па Парэта вектар
з крытэрыяльна мноства дамінуе па Парэта вектар 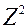 з таго ж мноства, калі
з таго ж мноства, калі 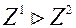 .
.
Не фармальна, мноства Парэта 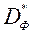 пастаўленай задачы многокритериальной аптымізацыі можна вызначыць як сукупнасць вектараў
пастаўленай задачы многокритериальной аптымізацыі можна вызначыць як сукупнасць вектараў 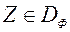 , Сярод якіх няма доминируемых. Фармальна, мноства Парэта вызначаюць наступным чынам:
, Сярод якіх няма доминируемых. Фармальна, мноства Парэта вызначаюць наступным чынам:
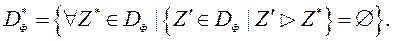
Калі 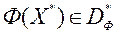 , То будзем казаць, што
, То будзем казаць, што 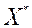 - эфектыўны па Парэта вектар. Мноства вектараў, якія належаць мноству Парэта, пазначым
- эфектыўны па Парэта вектар. Мноства вектараў, якія належаць мноству Парэта, пазначым 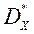 .
.
Інтэрактыўныя метады рашэння МКО-задачы заснаваныя на гіпотэзе існавання адзінай, невядомай ЛПР скалярнай функцыі яго пераваг 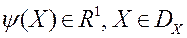 . Пры гэтым мяркуюць, што большага значэнні функцыі
. Пры гэтым мяркуюць, што большага значэнні функцыі 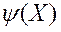 адпавядае больш пераважнае з пункту гледжання ЛПР рашэнне
адпавядае больш пераважнае з пункту гледжання ЛПР рашэнне 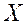 .
.
Метад FFANN. Першы інтэрактыўны метад многокритериальной аптымізацыі з выкарыстаннем нейронавых сетак для апраксімацыі функцыі пераваг ЛПР FFANN (Feed - Forward Artificial Neural Networks, метад з выкарыстаннем штучнай нейронных сеткі прамога распаўсюджвання) быў распрацаваны прафесарам Мінг Сан Універсітэта Тэхаса (г. Сан Антоніо, ЗША) і прафесарамі Антоніо стам і Ральф Штойер Універсітэта штата Джорджыя (г. Атланта, ЗША) [13].
У метадзе FFANN ЛПР ацэньвае прадстаўленыя яму рашэнні, задаючы канкрэтныя значэння сваёй функцыі пераваг па кожнаму асобнаму вырашэнню. Для палягчэння працэдуры ацэнкі, на кожнай ітэрацыі яму падаюць вектар Надзіра 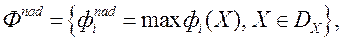 якому адпавядае значэнне функцыі пераваг
якому адпавядае значэнне функцыі пераваг 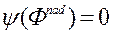 , І ідэальны вектар
, І ідэальны вектар 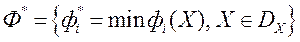 з ацэнкай
з ацэнкай 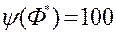 .
.
Структура нейронавы сеткі прадстаўлена на малюнку 1. ўваходы нейронавы сеткі з'яўляюцца кампаненты нармалізаванага вектара прыватных крытэрыяў аптымальнасці, выхадам - значэнне функцыі пераваг. Аўтары гэтага метаду правялі шэраг эксперыментаў, якія пацвярджаюць той факт, што метад з'яўляецца робастным да выбару архітэктуры нейронавай сеткі, дакладней кажучы, - да ліку нейронаў ў схаваным пласце.
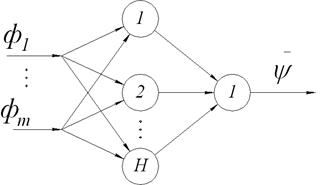
Малюнак 1 - Архітэктура нейронавай сеткі ў метадзе FFANN
Метад FFANN складаецца з наступных крокаў.
Крок 1. Генеруючы s недоминируемых вектараў 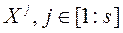 у мностве дапушчальных значэнняў
у мностве дапушчальных значэнняў 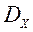 . Вылічаем значэння адпаведнага вектарнага крытэра аптымальнасці
. Вылічаем значэння адпаведнага вектарнага крытэра аптымальнасці 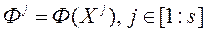 . Ініцыялізуючы лічыльнік колькасці ітэрацый
. Ініцыялізуючы лічыльнік колькасці ітэрацый 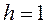 .
.
Крок 2. Прадстаўляем s значэнняў вектарнага крытэра аптымальнасці 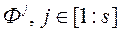 сумесна з вектарамі
сумесна з вектарамі 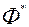 і
і 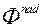 для ацэнкі ЛПР. На аснове атрыманай інфармацыі аб перавагах ЛПР, вызначаем найлепшы вектар
для ацэнкі ЛПР. На аснове атрыманай інфармацыі аб перавагах ЛПР, вызначаем найлепшы вектар 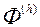 , Знойдзены сярод усіх ітэрацый. Калі ЛПР задавальняе бягучае найлепшае рашэнне, то гэтае рашэнне ЛПР прымае ў якасці рашэння МКО-задачы і спыняе вылічэнні.
, Знойдзены сярод усіх ітэрацый. Калі ЛПР задавальняе бягучае найлепшае рашэнне, то гэтае рашэнне ЛПР прымае ў якасці рашэння МКО-задачы і спыняе вылічэнні.
Крок 3. Нармалізуем кампаненты кожнага з s крытэрыяльна вектараў па формуле
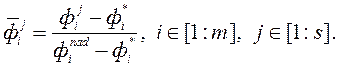
Крок 4. Пасля таго як ЛПР прызначыў кожнаму з рашэннем значэнне сваёй функцыі пераваг 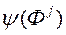 , Выконваем нармалізацыю яго ацэнак:
, Выконваем нармалізацыю яго ацэнак:
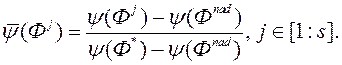
Крок 5. Выкарыстоўваючы нармалізаваныя вектары 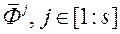 з адпаведнымі нармалізаваць ацэнкамі
з адпаведнымі нармалізаваць ацэнкамі 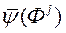 выконваем навучанне нейронавай сеткі FFANN.
выконваем навучанне нейронавай сеткі FFANN.
Крок 6. Выкарыстоўваючы выхады нейронных сеткі FFANN для вылічэнні значэнняў мэтавай функцыі, вырашаем задачу аптымізацыі для атрымання новага вэктару рашэнняў на бягучай h -ай ітэрацыі:
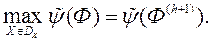
Крок 7. Калі значэнне вектарнага крытэра аптымальнасці 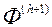 з'яўляецца унікальным, гэта значыць яго не прадастаўлялі ЛПР для ацэнкі на папярэдніх ітэрацый, то генеруючы новыя недоминируемые рашэння, колькасць якіх роўна (s -1). У адваротным выпадку, ігнаруем
з'яўляецца унікальным, гэта значыць яго не прадастаўлялі ЛПР для ацэнкі на папярэдніх ітэрацый, то генеруючы новыя недоминируемые рашэння, колькасць якіх роўна (s -1). У адваротным выпадку, ігнаруем 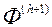 і генеруючы s новых рашэнняў. Пераходзім на Крок 2.
і генеруючы s новых рашэнняў. Пераходзім на Крок 2.
Для генерацыі недоминируемых рашэнняў аўтары метаду прапануюць выкарыстоўваць пашыраную узважаную скруткам Чебышева (augmented weighted Tchebycheff program)
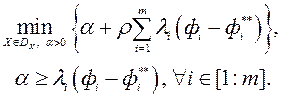
тут 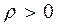 малая станоўчая канстанта; утапічны вектар
малая станоўчая канстанта; утапічны вектар 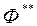 мае каардынаты
мае каардынаты 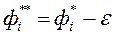 , дзе
, дзе 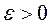 малая станоўчая канстанта. Вобласць дапушчальных значэнняў вектара вагавых множнікаў
малая станоўчая канстанта. Вобласць дапушчальных значэнняў вектара вагавых множнікаў 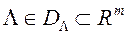 мае выгляд
мае выгляд 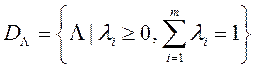 . Навучанне нейронавай сеткі адбываецца стандартным метадам зваротнага распаўсюджвання памылкі.
. Навучанне нейронавай сеткі адбываецца стандартным метадам зваротнага распаўсюджвання памылкі.
Асноўным недахопам дадзенага метаду з'яўляецца тое, што рашэнні, якія генерыруюцца нейронавай сеткай, не заўсёды з'яўляюцца Парэта аптымальнымі. Для вырашэння гэтай праблемы аўтары метаду FFANN прапанавалі мадыфікаваны варыянт дадзенага метаду, які носіць назву FFANN -2 [14].
Метад FFANN -2. Коратка разгледзім асноўныя адрозненні мадыфікаванага метаду FFANN -2 ад яго арыгінальнай версіі. У метадзе FFANN -2 адвольным чынам генеруючы 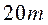 вагавых вектараў
вагавых вектараў 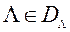 , Дзе m - лік прыватных крытэрыяў аптымальнасці. Аўтары метаду рэкамендуюць выкарыстоўваць лік рашэнняў роўнае
, Дзе m - лік прыватных крытэрыяў аптымальнасці. Аўтары метаду рэкамендуюць выкарыстоўваць лік рашэнняў роўнае 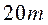 , На аснове праведзенага імі эмпірычнага даследавання. далей сярод
, На аснове праведзенага імі эмпірычнага даследавання. далей сярод 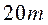 вагавых вектараў выбіраем 2 s вектара найбольш аддаленых адзін ад аднаго на фронце Парэта. Пасля гэтага, выкарыстоўваючы выхад навучанай нейронавай сеткі
вагавых вектараў выбіраем 2 s вектара найбольш аддаленых адзін ад аднаго на фронце Парэта. Пасля гэтага, выкарыстоўваючы выхад навучанай нейронавай сеткі 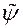 у якасці значэння функцыі пераваг ЛПР, вылічаем значэння функцыі
у якасці значэння функцыі пераваг ЛПР, вылічаем значэння функцыі 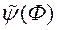 пры падачы на ўваход 2 s вектараў
пры падачы на ўваход 2 s вектараў 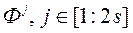 . Сярод усіх атрыманых значэнняў
. Сярод усіх атрыманых значэнняў 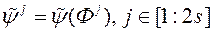 выбіраем s вектараў
выбіраем s вектараў 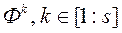 , Якія забяспечваюць максімальнае значэнне
, Якія забяспечваюць максімальнае значэнне 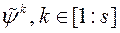 .
.
У дадзенай версіі метаду нейронных сетку, якая рэалізуе апраксімацыю функцыі пераваг ЛПР, не ўдзельнічае ў пошуку найлепшага з пункту гледжання ЛПР рашэння, яна ўсяго толькі ўяўляе сабой аператар, які падтрымлівае разнастайнасць рашэнняў, якія прадстаўляюцца ЛПР для ацэнкі.
Метад PREF (PREFerence) закліканы вырашыць вышэйпаказаныя недахопы метадаў FFANN. Дадзены метад быў распрацаваны аўтарам агляду пад кіраўніцтвам д.ф.-м.н. Карпенка А.П. у МГТУ ім. Н.Э. Баумана [15].
У аснове метаду PREF ляжыць аперацыя скалярнай скруткі прыватных крытэрыяў аптымальнасці 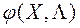 , дзе
, дзе 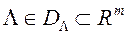 - вектар вагавых множнікаў,
- вектар вагавых множнікаў, 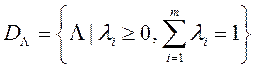 - мноства дапушчальных значэнняў гэтага вэктару. Спосаб скруткі ня фіксуецца - гэта можа быць адытыўная скрутка, мультыплікатыўны скрутка і іншыя.
- мноства дапушчальных значэнняў гэтага вэктару. Спосаб скруткі ня фіксуецца - гэта можа быць адытыўная скрутка, мультыплікатыўны скрутка і іншыя.
Пры кожным фіксаваным вектары 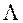 метад скалярнай скруткі зводзіць рашэнне многокритериальной задачы (1) да вырашэння однокритериальной задачы глабальнай ўмоўнай аптымізацыі (ОКО-задачы)
метад скалярнай скруткі зводзіць рашэнне многокритериальной задачы (1) да вырашэння однокритериальной задачы глабальнай ўмоўнай аптымізацыі (ОКО-задачы)
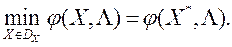
(2)
З-за абмежаванасці і замкнёнасці мноства 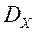 рашэнне задачы (2) існуе.
рашэнне задачы (2) існуе.
Калі пры кожным 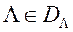 рашэнне задачы (2) адзіна, то ўмова (2) ставіць у адпаведнасць кожнаму з дапушчальных вектараў
рашэнне задачы (2) адзіна, то ўмова (2) ставіць у адпаведнасць кожнаму з дапушчальных вектараў 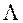 адзіны вектар
адзіны вектар 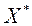 і адпаведныя значэння прыватных крытэрыяў аптымальнасці
і адпаведныя значэння прыватных крытэрыяў аптымальнасці 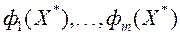 . Гэтая акалічнасць дазваляе меркаваць, што функцыя пераваг ЛПР
. Гэтая акалічнасць дазваляе меркаваць, што функцыя пераваг ЛПР 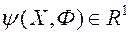 вызначана ня на мностве
вызначана ня на мностве 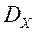 , А на мностве
, А на мностве 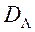 .
.
Асноўная ідэя метаду PREF заключаецца ў пабудове апраксімацыі функцыі пераваг ЛПР 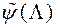 на мностве
на мностве 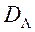 і пошуку вэктару
і пошуку вэктару 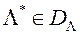 , Які максімізуе функцыю пераваг ЛПР. Больш строга, вектар
, Які максімізуе функцыю пераваг ЛПР. Больш строга, вектар 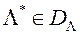 знаходзім у выніку рашэння ОКО-задачы
знаходзім у выніку рашэння ОКО-задачы
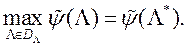
Пераход з прасторы варьируемых параметраў 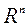 , У прастору вагавых множнікаў
, У прастору вагавых множнікаў 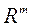 , Дазваляе спрасціць пошук найлепшага з пункту гледжання ЛПР рашэння, паколькі, як правіла
, Дазваляе спрасціць пошук найлепшага з пункту гледжання ЛПР рашэння, паколькі, як правіла 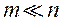 .
.
Ключавой працэдурай ў метадзе PREF з'яўляецца апраксімацыя функцыі пераваг. Для апраксімацыі функцыі пераваг у працы [15] прапанавана выкарыстоўваць нейронавыя сеткі, апарат невыразнай логікі і нейра-недакладныя сістэмы.
Агульная схема метаду PREF з'яўляецца ітэрацыйныя і складаецца з наступных асноўных этапаў.
Этап «разгону» метаду. МКО-сістэма нейкім чынам (напрыклад, выпадкова) паслядоўна генеруе k вектараў 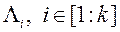 і для кожнага з гэтых вектараў выконвае наступныя дзеянні.
і для кожнага з гэтых вектараў выконвае наступныя дзеянні.
1) Вырашае ОКО-задачу
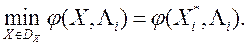
(3)
2) прад'яўляюцца ЛПР знойдзенае рашэнне 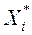 , А таксама адпаведныя значэнне ўсіх прыватных крытэрыяў аптымальнасці
, А таксама адпаведныя значэнне ўсіх прыватных крытэрыяў аптымальнасці 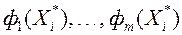 .
.
3) ЛПР ацэньвае гэтыя дадзеныя і ўводзіць у МКО-сістэму адпаведнае значэнне сваёй функцыі пераваг 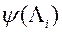 .
.
Першы этап. На аснове ўсіх наяўных у МКО-сістэме значэнняў 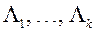 вэктару
вэктару 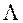 і адпаведных адзнак функцыі пераваг
і адпаведных адзнак функцыі пераваг 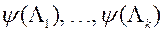 МКО-сістэма выконвае наступныя дзеянні.
МКО-сістэма выконвае наступныя дзеянні.
1) Будуе функцыю 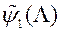 , Апраксімуецца функцыю
, Апраксімуецца функцыю 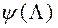 ў наваколлі кропак
ў наваколлі кропак 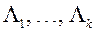 .
.
2) адшуквалі максімум функцыі 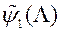 - вырашае ОКО-задачу
- вырашае ОКО-задачу
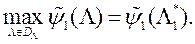
3) З знойдзеных вектарам 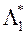 вырашае ОКО-задачу віду (3) - знаходзіць вектар параметраў і адпаведныя значэння прыватных крытэрыяў аптымальнасці, а затым прад'яўляе іх ЛПР. У сваю чаргу, ЛПР ацэньвае прапанаваныя яму рашэнні і ўводзіць у сістэму адпаведнае значэнне сваёй функцыі пераваг
вырашае ОКО-задачу віду (3) - знаходзіць вектар параметраў і адпаведныя значэння прыватных крытэрыяў аптымальнасці, а затым прад'яўляе іх ЛПР. У сваю чаргу, ЛПР ацэньвае прапанаваныя яму рашэнні і ўводзіць у сістэму адпаведнае значэнне сваёй функцыі пераваг 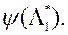
Другі этап. На аснове ўсіх наяўных у сістэме значэнняў вэктару 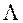 і адпаведных адзнак функцыі пераваг
і адпаведных адзнак функцыі пераваг 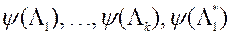 МКО-сістэма выконвае апраксімацыю функцыі
МКО-сістэма выконвае апраксімацыю функцыі 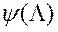 ў наваколлі кропак
ў наваколлі кропак 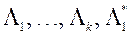 - будуе функцыю
- будуе функцыю 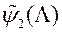 . І гэтак далей па схеме першага этапу да таго часу, пакуль ЛПР не спыніцца на якім-небудзь рашэнні.
. І гэтак далей па схеме першага этапу да таго часу, пакуль ЛПР не спыніцца на якім-небудзь рашэнні.
Такім чынам, у метадзе PREF на этапе аналізу ЛПР для ацэнкі падаюцца рашэння, якія належаць мноству Парэта. На этапе разліку для пошуку больш здавальняючых з пункту гледжання ЛПР рашэнняў непасрэдна выкарыстоўваецца апраксімацыя функцыі пераваг ЛПР.
Асаблівасці нейросетевая, невыразнай і нейра-невыразнай апраксімацыі функцыі пераваг ЛПР разглядаюцца ў працах [16, 17, 18]. Таксама ў гэтых працах праведзена даследаванне эфектыўнасці названых спосабаў апраксімацыі пры вырашэнні тэставых МКО-задач. Вынікі рашэння практычных задач з выкарыстаннем метаду PREF прадстаўленыя ў працах [16, 19].
У разгляданым класе метадаў мяркуюць, што ЛПР ўносіць свае перавагі ў МКО-сістэму ў выглядзе парнага параўнання асобных рашэнняў [20, 21, 22]. Напрыклад, альтэрнатыва ![У разгляданым класе метадаў мяркуюць, што ЛПР ўносіць свае перавагі ў МКО-сістэму ў выглядзе парнага параўнання асобных рашэнняў [20, 21, 22]](/wp-content/uploads/2019/12/be-navuka-i-adukacyu-90.gif) і адпаведнае значэнне вектарнага крытэра аптымальнасці
і адпаведнае значэнне вектарнага крытэра аптымальнасці 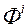 «Лепш» набору
«Лепш» набору 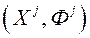 (Пазначым,
(Пазначым, 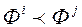 ) Або два набору
) Або два набору 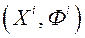 і
і 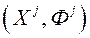 «Неадметныя»
«Неадметныя» 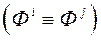 . На аснове атрыманай інфармацыі МКО-сістэма тым ці іншым спосабам будуе апраксімацыю функцыі пераваг ЛПР
. На аснове атрыманай інфармацыі МКО-сістэма тым ці іншым спосабам будуе апраксімацыю функцыі пераваг ЛПР 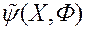 з мэтай забеспячэння карэктнага ранжыравання дадзеных. Іншымі словамі, калі
з мэтай забеспячэння карэктнага ранжыравання дадзеных. Іншымі словамі, калі 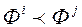 , то
, то 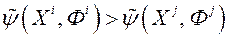 ; калі
; калі 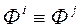 , то
, то 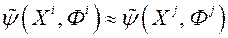 .
.
Усе метады дадзенага класа, распрацаваныя да цяперашняга часу, выкарыстоўваюць блізкі падыход, які складаецца ў камбінацыі аднаго з эвалюцыйных алгарытмаў з працэдурай пабудовы функцыі пераваг ЛПР 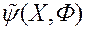 .
.
Агульная схема метадаў дадзенага класа можа быць прадстаўлена наступным чынам.
Крок 1. Генеруючы пачатковую папуляцыю рашэнняў 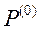 .
.
Крок 2. Адным з метадаў набліжанага пабудовы мноства Парэта атрымліваем пачатковую апраксімацыю гэтага мноства: фарміруем мноства рашэнняў 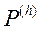 .
.
Крок 3. Выбіраем з мноства 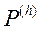 колькасць рашэнняў
колькасць рашэнняў 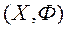 роўнае s для ацэнкі ЛПР. Затым ЛПР ранжыруе гэтыя рашэнні і ўносіць гэтую інфармацыю ў сістэму.
роўнае s для ацэнкі ЛПР. Затым ЛПР ранжыруе гэтыя рашэнні і ўносіць гэтую інфармацыю ў сістэму.
Крок 4. На аснове атрыманай інфармацыі МКО-сістэма будуе апраксімацыю функцыі пераваг ЛПР 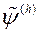 .
.
Крок 5. Запускаем метад набліжанага пабудовы мноства Парэта, пры гэтым, у якасці «функцыі прыстасаванасці» асобных рашэнняў выкарыстоўваем бягучую функцыю пераваг ЛПР 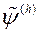 і фарміруем мноства рашэнняў
і фарміруем мноства рашэнняў 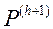 .
.
Крок 6. Калі ўмова супыну выканана, то завяршаем вылічэнні. У адваротным выпадку, ажыццяўляем пераход на Крок 2.
Асноўным крытэрыем супыну з'яўляецца атрыманне ЛПР найбольш задавальняе Яго рашэнні. Аднака на этапе выпрабаванні метаду на тэставых задачах многокритериальной аптымізацыі, пры адсутнасці рэальнага ЛПР, могуць Быць разгледжаны таксама іншыя ўмовы. Напрыклад, выкананне наперад зададзенага ліку ітэрацый дыялогу з ЛПР або дасягненне фіксаванага колькасці ітэрацый метаду набліжанага пабудовы мноства Парэта.
Далей у працы разглядаем найбольш развітыя сучасныя метады дадзенага класа: IEM, PI - EMO - VF, BC - EMO.
Метад IEM. У працы [20] аўтары прапануюць метад IEM (Interactive Evolutionary Method, Інтэрактыўны эвалюцыйны метад), у аснове якога ляжыць скалярная скрутка прыватных крытэрыяў аптымальнасці выгляду
![У працы [20] аўтары прапануюць метад IEM (Interactive Evolutionary Method, Інтэрактыўны эвалюцыйны метад), у аснове якога ляжыць скалярная скрутка прыватных крытэрыяў аптымальнасці выгляду](/wp-content/uploads/2019/12/be-navuka-i-adukacyu-105.gif)
(4)
Дзе 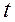 - параметр, які вызначае функцыю пераваг;
- параметр, які вызначае функцыю пераваг; 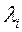 - кампаненты вектара вагавых множнікаў
- кампаненты вектара вагавых множнікаў 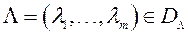 ;
; 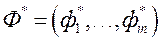 - ідэальны вектар прыватных крытэрыяў аптымальнасці. Для знаходжання вагавых множнікаў
- ідэальны вектар прыватных крытэрыяў аптымальнасці. Для знаходжання вагавых множнікаў 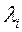 аўтары вырашаюць задачу аптымізацыі
аўтары вырашаюць задачу аптымізацыі
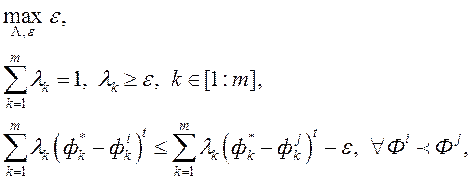
(5)
Дзе 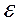 - «мяжа» пераваг. Тут парныя параўнання рашэнняў фармуюць абмежаванні задачы аптымізацыі. У працы [20] аўтары мяркуюць, што функцыя пераваг ЛПР лінейная (
- «мяжа» пераваг. Тут парныя параўнання рашэнняў фармуюць абмежаванні задачы аптымізацыі. У працы [20] аўтары мяркуюць, што функцыя пераваг ЛПР лінейная ( 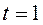 ). Пры гэтым, аўтары не прыводзяць ніякіх рэкамендацый па выбары гэтага параметру. Калі функцыя пераваг нелінейная, то гэты метад можа генераваць недапушчальныя для ЛПР рашэння. У гэтым выпадку аўтары прапануюць выдаляць па адным з абмежаванняў у храналагічным парадку, да таго часу, пакуль рашэнне задачы (5) не будзе знойдзена. Тым самым яны мяркуюць, што апошнія паступілі ацэнкі ад ЛПР маюць б аб льшую важнасць, чым інфармацыя, атрыманая на першых ітэрацыі.
). Пры гэтым, аўтары не прыводзяць ніякіх рэкамендацый па выбары гэтага параметру. Калі функцыя пераваг нелінейная, то гэты метад можа генераваць недапушчальныя для ЛПР рашэння. У гэтым выпадку аўтары прапануюць выдаляць па адным з абмежаванняў у храналагічным парадку, да таго часу, пакуль рашэнне задачы (5) не будзе знойдзена. Тым самым яны мяркуюць, што апошнія паступілі ацэнкі ад ЛПР маюць б аб льшую важнасць, чым інфармацыя, атрыманая на першых ітэрацыі.
Метад PI - EMO - VF (Progressively Interactive Evolutionary Multi - objective Optimization using Value Function, Інтэрактыўны Эвалюцыйны метад Многокритериальный Аптымізацыі з выкарыстаннем Функцыі Асаблівых) [21]. Тут аўтары прапануюць выкарыстоўваць функцыю пераваг выгляду
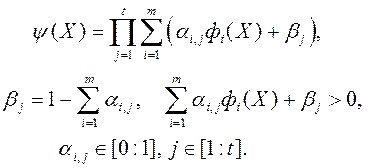
(6)
Параметр t таксама вызначае функцыю пераваг ЛПР. вызначэнне каэфіцыентаў 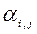 І
І 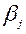 адбываецца ў выніку рашэння дапаможнай задачы
адбываецца ў выніку рашэння дапаможнай задачы
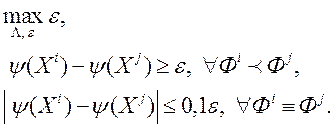
(7)
У адрозненне ад метаду IEM, тут ўлічваецца інфармацыя аб рашэннях, якія для ЛПР раўназначныя. Іншым важным адрозненнем, з'яўляецца тое, што параметр 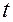 падбіраюць ітэрацыйныя. На першым этапе прымаюць
падбіраюць ітэрацыйныя. На першым этапе прымаюць 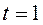 і вырашаюць задачу (7). Калі ў працэсе вырашэння гэтай задачы не ўдаецца знайсці каэфіцыенты функцыі пераваг (6) так, каб задаволіць ўсім абмежаванням, то параметр
і вырашаюць задачу (7). Калі ў працэсе вырашэння гэтай задачы не ўдаецца знайсці каэфіцыенты функцыі пераваг (6) так, каб задаволіць ўсім абмежаванням, то параметр 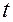 павялічваюць
павялічваюць 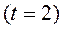 , І зноў вырашаюць задачу (7). Вылічэнні выконваюць да таго часу, пакуль функцыя пераваг не будзе задавальняць усім абмежаванняў (7).
, І зноў вырашаюць задачу (7). Вылічэнні выконваюць да таго часу, пакуль функцыя пераваг не будзе задавальняць усім абмежаванняў (7).
Метад PI - EMO - VF ў якасці метаду апраксімацыі мноства Парэта выкарыстоўвае алгарытм NSGA - II (Non-dominated sorting genetic algorithm version II - Генетычны алгарытм недоминируемой сартавання версіі II) [23].
Аўтары метадаў IEM і PI - EMO - VF пры пабудове функцыі пераваг не прымаюць пад увагу тое, што ЛПР можа памыляцца і даваць супярэчлівыя адказы. Яны маюць на ўвазе, што ЛПР заўсёды дае верныя ацэнкі і, у выніку, зводзяць задачу навучання да задачы аптымізацыі.
Метад BC - EMO (Brain - Computer Evolutionary Multiobjective Optimization, Нейрокомпьютерная Эвалюцыйны метад Многокритериальной Аптымізацыі), з нашага пункту гледжання, з'яўляецца найбольш перспектыўным у цяперашні час [22]. Адзначым, што пераклад тэрміна «brain-computer» адпавядае прынятай тэрміналогіі (http://neurobotics.ru/research/bci/). Апраксімацыю функцыі пераваг ![Метад BC - EMO (Brain - Computer Evolutionary Multiobjective Optimization, Нейрокомпьютерная Эвалюцыйны метад Многокритериальной Аптымізацыі), з нашага пункту гледжання, з'яўляецца найбольш перспектыўным у цяперашні час [22]](/wp-content/uploads/2019/12/be-navuka-i-adukacyu-119.gif) у гэтым метадзе выконваюць на аснове машыны апорных вектараў (Support Vector Machine, SVM) [24], што выгадна адрознівае BC - EMO ад астатніх існуючых інтэрактыўных метадаў дадзенага класа:
у гэтым метадзе выконваюць на аснове машыны апорных вектараў (Support Vector Machine, SVM) [24], што выгадна адрознівае BC - EMO ад астатніх існуючых інтэрактыўных метадаў дадзенага класа:
1) метад дазваляе будаваць функцыю пераваг на аснове парных параўнанняў рашэнняў, гэтая форма ацэнкі рашэнняў з'яўляецца найбольш зручнай для ЛПР;
2) метад з'яўляецца робастным да недакладным і супярэчлівым ацэнак ЛПР, што з'яўляецца тыповым пры вырашэнні МКО-задач;
3) выбар розных ядраў [24] ў метадзе апорных вектараў дазваляе найлепшым спосабам аппроксимировать функцыю пераваг ЛПР.
У метадзе BC - EMO функцыя пераваг ЛПР будуецца ў выглядзе 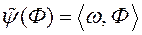 , Дзе сімвал
, Дзе сімвал 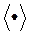 пазначае скалярны твор вектараў. Гэтая функцыя павінна выконваць зададзенае ранжыраванне дадзеных:
пазначае скалярны твор вектараў. Гэтая функцыя павінна выконваць зададзенае ранжыраванне дадзеных: 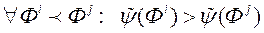 . Для пабудовы функцыі пераваг ЛПР неабходна знайсці такі вектар
. Для пабудовы функцыі пераваг ЛПР неабходна знайсці такі вектар 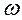 , Які задавальняе ўсім няроўнасць віду
, Які задавальняе ўсім няроўнасць віду
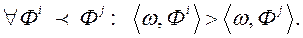
(8)
Пры вырашэнні практычных задач вельмі складана падабраць такі вектар 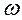 , Які задавальняе ўсім вышэйпаказаным няроўнасць (8). У гэтым выпадку, кропкі з прасторы крытэрыяў праецыююць ў новую прастору прыкмет (feature space) пры дапамозе праецыююць функцыі
, Які задавальняе ўсім вышэйпаказаным няроўнасць (8). У гэтым выпадку, кропкі з прасторы крытэрыяў праецыююць ў новую прастору прыкмет (feature space) пры дапамозе праецыююць функцыі 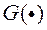 . Новую прастору мае вялікую памернасць, чым памернасць прасторы крытэраў (гэта прастора, у якім да зыходных прыкметах - прыватным крытэрам аптымальнасці - дададзеныя іх парныя творы). У матэматычнай фармулёўцы задача аптымізацыі для пошуку вэктару
. Новую прастору мае вялікую памернасць, чым памернасць прасторы крытэраў (гэта прастора, у якім да зыходных прыкметах - прыватным крытэрам аптымальнасці - дададзеныя іх парныя творы). У матэматычнай фармулёўцы задача аптымізацыі для пошуку вэктару 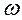 мае выгляд
мае выгляд
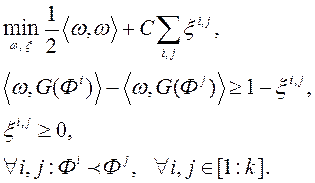
(9)
фіктыўная пераменная ![фіктыўная пераменная характарызуе велічыню памылкі на двух вектарах І , З - параметр рэгулярызацыі, задаецца карыстальнікам або адаптыўна падбіраецца на аснове крыжаванай праверкі (cross-validation) [22]](/wp-content/uploads/2019/12/be-navuka-i-adukacyu-127.gif) характарызуе велічыню памылкі на двух вектарах
характарызуе велічыню памылкі на двух вектарах 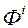 І
І 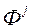 , З - параметр рэгулярызацыі, задаецца карыстальнікам або адаптыўна падбіраецца на аснове крыжаванай праверкі (cross-validation) [22].
, З - параметр рэгулярызацыі, задаецца карыстальнікам або адаптыўна падбіраецца на аснове крыжаванай праверкі (cross-validation) [22].
Задача (9) з'яўляецца задачай квадратычнага праграмавання, таму для яе вырашэння мэтазгодна ўжыць метад множнікаў Лагранжа. Метад патрабуе вылічэнні скалярнага творы 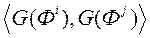 . Для эфектыўнага вылічэнні скалярнага творы двух вектараў без непасрэднага праецыравання іх у новую прастору ўводзяць паняцце ядра скалярнага творы і абазначаюць яго
. Для эфектыўнага вылічэнні скалярнага творы двух вектараў без непасрэднага праецыравання іх у новую прастору ўводзяць паняцце ядра скалярнага творы і абазначаюць яго 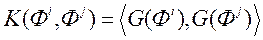 .
.
У выніку функцыю пераваг можна запісаць у выглядзе лінейнай камбінацыі ядраў
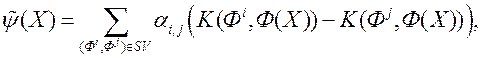
Дзе ![Дзе - множнікі Лагранжа [22]](/wp-content/uploads/2019/12/be-navuka-i-adukacyu-133.gif) - множнікі Лагранжа [22].
- множнікі Лагранжа [22].
У метадзе BC - EMO выбар канкрэтнай функцыі ядра адбываецца аўтаматычна ў працэсе вырашэння МКО-задачы на аснове крыжаванай праверкі з наступнага спісу:
· 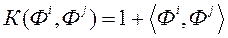 - лінейная функцыя;
- лінейная функцыя;
· 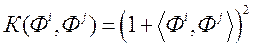 - паліномны функцыя другой ступені;
- паліномны функцыя другой ступені;
· 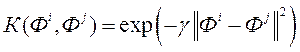 - гауссова функцыя, дзе станоўчую канстанту
- гауссова функцыя, дзе станоўчую канстанту 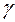 падбіраюць з сукупнасці
падбіраюць з сукупнасці 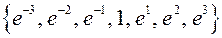 .
.
Арыгінальная версія BC - EMO, таксама як метад PI - EMO - VF, у якасці метаду апраксімацыі мноства Парэта выкарыстоўвае алгарытм NSGA - II [23].
Вынікі шырокага даследавання эфектыўнасці метаду BC - EMO на розных тэставых МКО-задачах прыведзены ў рабоце [22].
У працы выкананы агляд сучасных інтэрактыўных метадаў FFANN і PREF, заснаваных на ацэнках функцыі пераваг, і метадаў IEM, PI - EMO - VF і BC - EMO, заснаваных на парным параўнанні рашэнняў.
На падставе выкананага агляду можа быць зроблена выснова аб тым, што найбольш перспектыўнымі з'яўляюцца метады PREF і BC - EMO. Прапануюцца наступныя напрамкі развіцця гэтых метадаў.
· Распрацоўка больш зручных сродкаў ўзаемадзеяння ЛПР з названымі метадамі; стварэнне самастойнай МКО-сістэмы на аснове гэтых метадаў.
· Распрацоўка і рэалізацыя паралельных алгарытмаў метадаў PREF і BC - EMO ў сувязі з тым, што практычныя задачы аптымізацыі, як правіла, маюць вялікую вылічальную складанасць.
Аўтар дзякуе свайго навуковага кіраўніка д.ф.-м.н. МГТУ им.Н.Э. Баумана Карпенка А.П. за плённае абмеркаванне працы, а таксама за ўсебаковую дапамогу па яе ўдасканаленні.
Спіс літаратуры
1. лотаў А.В., Паспелава І.І. Многокритериальные задачы прыняцця рашэнняў: вучэб. дапаможнік. М .: МАКС Прэс, 2008. 197 c.
2. Растригин Л.А., Эйдук Я.Ю. Адаптыўныя метады многокритериальной аптымізацыі // Аўтаматыка і тэлемеханікі. 1985. № 1. С. 5-26.
3. Wierzbicki AP Reference point approaches // Multicriteria Decision Making: Advances in MCDM Models, Algorithms, Theory and Applications / Gal T., Stewart TJ, Hanne T. (Eds.). Boston: Kluwer Academic Publishers, 1999. P. 9.1-9.39.
4. Карпенка А. П., Семяніхін А. С., Міціна Е. У. Папуляцыйныя метады апраксімацыі мноства Парэта ў задачы многокритериальной аптымізацыі. Агляд // Навука і адукацыя. МГТУ ім. Н.Э. Баумана. Электрон. Журня. 2012. № 4. Рэжым доступу: http://www.technomag.edu.ru/doc/363023.html (Дата звароту 08.07.2012).
5. Multiobjective Optimization: Interactive and Evolutionary Approaches / Branke J., Deb K., Miettinen K., Slowinski R. (Eds.). Berlin / Heidelberg, Germany: Springer-Verlag, 2008. 470 p.
6. Wang R., Purshouse RC, Fleming PJ Preference-inspired Co-evolutionary Algorithms for Many-objective Optimisation // IEEE Transactions on Evolutionary Computation. 2012. DOI: 10.1109 / TEVC.2012.2204264
7. Miettinen K. Nonlinear Multiobjective Optimization. Boston: Kluwer Academic Publishers, 1999. 298 p.
8. Gass S., Saaty T. The computational algorithm for the parametric objective function // Naval Research Logistics Quarterly. Wiley, 1955. Vol. 2, no. 1-2. P. 39-45.
9. Fishburn PC Lexicographic orders, utilities and decision rules: A survey // Management Science. USA, 1974. Vol. 20, no. 11. P. 1442-1471.
10. Charnes A., Cooper WW Management Models and Industrial Applications of Linear Programming. Vol. 1. New York: Wiley, 1961. 859 p.
11. Ларычаў А.І. Тэорыя і метады прыняцця рашэнняў. М .: Універсітэцкая кніга, Логас, 2002. 392 c.
12. Miettinen K., Makela MM Interactive Bundle-based Method for Nondifferentiable Multiobjective Optimization: NIMBUS // Optimization: A Journal of Mathematical Programming and Operations Research. 1995. Vol. 34, no. 3. P. 231-246.
13. Sun M., Stam A., Steuer R. Solving multiple objective programming problems using feed-forward artificial neural networks: The interactive FFANN procedure // Management Science. 1996. Vol. 42, no. 6. P. 835-849.
14. Sun M., Stam A., Steuer R. Interactive multiple objective programming using Tchebycheff programs and artificial neural networks // Computer Operations Research. 2000. Vol. 27, no. 7-8. P. 601-620.
15. Карпенка А.П., Хведарук В.Г. Апраксімацыя функцыі пераваг асобы, які прымае рашэнні, у задачы многокритериальной аптымізацыі. 3. Метады на аснове нейронавых сетак і невыразнай логікі // Навука і адукацыя. МГТУ ім. Н.Э. Баумана. Электрон. Журня. 2008. № 4. Рэжым доступу: http://www.technomag.edu.ru/doc/86335.html (Дата звароту 02.07.2012).
16. Карпенка А.П., Мухлисуллина Д.Т., Аўчыннікаў В.А. Нейросетевая апраксімацыя функцыі пераваг асобы, які прымае рашэнні, у задачы многокритериальной аптымізацыі // Інфармацыйныя тэхналогіі. 2010. № 10. С. 2-9.
17. Карпенка А.П., Моор Д.А., Мухлисуллина Д.Т. Многокритериальная аптымізацыя на аснове невыразнай апраксімацыі функцыі пераваг асобы, які прымае рашэнні // Навукаёмістыя тэхналогіі і інтэлектуальныя сістэмы -2010: працы 12-ай моладзевай міжнароднай навукова-тэхнічнай канферэнцыі. М., 2010. С. 94-98.
18. Карпенка А.П., Моор Д.А., Мухлисуллина Д.Т. Многокритериальная аптымізацыя на аснове нейра-невыразнай апраксімацыі функцыі пераваг асобы, які прымае рашэнні // Навука і адукацыя. МГТУ ім. Н.Э. Баумана. Электрон. Журня. 2010. № 6. Рэжым доступу: http://technomag.edu.ru/doc/143964.html (Дата звароту 2012/10/03).
19. Карпенка А.П., Мухлисуллина Д.Т., Цвяткоў А.А. Многокритериальная аптымізацыя геаметрыі шчыліннага фільтра для ачысткі вадкасцяў // Навука і адукацыя. МГТУ ім. Н. Э. Баумана. Электрон. Журня. 2013. № 2. DOI: 10.7463 / 0213.0539055
20. Phelps S., Koksalan M. An interactive evolutionary metaheuristic for multiobjective combinatorial optimization // Management Science. 2003. Vol. 49, no. 12. P. 1726-1738.
21. Deb K., Sinha A., Korhonen PJ, Wallenius J. An Interactive Evolutionary Multiobjective Optimization Method Based on Progressively Approximated Value Function // IEEE Transactions on Evolutionary Computation. 2010. Vol. 14, no. 5. P. 723-739.
22. Battiti R., Passerini A. Brain-computer evolutionary multiobjective optimization (BC-EMO): a genetic algorithm adapting to the decision maker // IEEE Transaction on Evolutionary Computation. 2010. Vol. 14, no. 5. P. 671-687.
23. Deb K., Pratap A., Agarwal S., Meyarivan T. A fast elitist multi-objective genetic algorithm: NSGA-II // IEEE Transaction on Evolutionary Computation. 2002. Vol. 6, no. 2. P. 182-197.
24. Хайкин С. Нейронавыя сеткі. Поўны курс: зав. в е англ. М .: ТАА «И.Д.Вильямс», 2008. 1104 c.
25. Zhang Q., Li H. MOEA / D: A multiobjective evolutionary algorithm based on decomposition // IEEE Transactions on Evolutionary Computation. 2007. Vol. 11, no. 6. P. 712-731.
26. Li H., Zhang Q. Multiobjective optimization problems with complicated pareto sets, MOEA / D and NSGA-II // IEEE Transactions on Evolutionary Computation. 2009. Vol. 13, no. 2. P. 284-302.
